Rate of Reaction:
Order of Reaction

For reaction aA + bB + ….. → cC+ ….

|
For reaction aA + bB + ….. → cC+ ….
R ∝[A]m[B]n or R = k[A]m[B]n….
Where m and n may or may not be equal to a & b.
m is order of reaction with respect to A and n is the order of reaction with respect to B.
m + n +… is the overall order of the reaction.
Elementary Reaction:
-
It is the reaction which completes in a single step.
-
A reaction may involve more than one elementary reactions or steps also.
-
Overall rate of reaction depends on the slowest elementary step and thus it is known as rate determining step.
It is the reaction which completes in a single step.
A reaction may involve more than one elementary reactions or steps also.
Overall rate of reaction depends on the slowest elementary step and thus it is known as rate determining step.
Molecularity of Reaction:
-
Number of molecules taking part in an elementary step is known as its molecularity.
-
Order of an elementary reaction is always equal to its molecularity.
-
Elementary reactions with molecularity greater than three are not known because collisions in which more than three particles come together simultaneously are rare.
Number of molecules taking part in an elementary step is known as its molecularity.
Order of an elementary reaction is always equal to its molecularity.
Elementary reactions with molecularity greater than three are not known because collisions in which more than three particles come together simultaneously are rare.
Chemical Reaction
Molecularity
PCl5 → PCl3 + Cl2
Unimolecular
2HI → H2 + I2
Bimolecular
2SO2 + O2 → 2SO3
Trimolecular
NO + O3 → NO2 + O2
Bimolecular
2CO + O2 → 2CO2
Trimolecular
2FeCl3 + SnCl2 → SnCl2 + 2FeCl2
Trimolecular
PCl5 → PCl3 + Cl2
|
Unimolecular
|
2HI → H2 + I2
|
Bimolecular
|
2SO2 + O2 → 2SO3
|
Trimolecular
|
NO + O3 → NO2 + O2
|
Bimolecular
|
2CO + O2 → 2CO2
|
Trimolecular
|
2FeCl3 + SnCl2 → SnCl2 + 2FeCl2
|
Trimolecular
|
Differential and Integrated Rate Laws:
Zero Order Reactions:
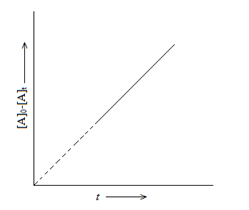 For Reaction: A → Product
[A]0-[A]t = k0t
Where,
[A]0 = Initial concentration of A
[A]t = Concentration of A at time t.
k0 = Rate constant for zero order reaction.
Half Life:
For Reaction: A → Product
[A]0-[A]t = k0t
Where,
[A]0 = Initial concentration of A
[A]t = Concentration of A at time t.
k0 = Rate constant for zero order reaction.
Half Life:

For Reaction: A → Product
[A]0-[A]t = k0t
Where,
[A]0 = Initial concentration of A
[A]t = Concentration of A at time t.
k0 = Rate constant for zero order reaction.
Half Life:
t1/2 = [A]0/2k
Unit of rate constant = mol dm-3s-1
Examples:
-
Enzyme catalyzed reactions are zero order with respect to substrate concentration.
-
Decomposition of gases on the surface of metallic catalysts like decomposition of HI on gold surface.
Examples:
Enzyme catalyzed reactions are zero order with respect to substrate concentration.
Decomposition of gases on the surface of metallic catalysts like decomposition of HI on gold surface.
First Order Reactions:
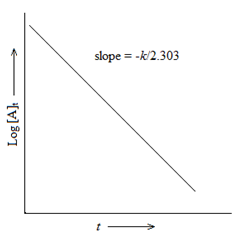 A → Product
(Δ [A] /A) = -k1Δt
or k1=( 2.303/ t)log ([A]0 / [A]t)
Half Life:
t1/2 = 0.693/k1
Half life is independent of the initial concentration of the reactant for a first order reaction.
Units of k1 = s-1
Examples:
N2O5 → 2NO2 + 1/2O2
Br2 → 2Br
2HNO3 → 2NO + H2O
H2O2→ H2O + 1/2O2
A → Product
(Δ [A] /A) = -k1Δt
or k1=( 2.303/ t)log ([A]0 / [A]t)
Half Life:
t1/2 = 0.693/k1
Half life is independent of the initial concentration of the reactant for a first order reaction.
Units of k1 = s-1
Examples:
N2O5 → 2NO2 + 1/2O2
Br2 → 2Br
2HNO3 → 2NO + H2O
H2O2→ H2O + 1/2O2

A → Product
(Δ [A] /A) = -k1Δt
or k1=( 2.303/ t)log ([A]0 / [A]t)
Half Life:
t1/2 = 0.693/k1
Half life is independent of the initial concentration of the reactant for a first order reaction.
Units of k1 = s-1
Examples:
N2O5 → 2NO2 + 1/2O2
Br2 → 2Br
2HNO3 → 2NO + H2O
H2O2→ H2O + 1/2O2
Pseudo First Order Reactions:
These are the reactions in which more than one species is involved in the rate determining step but still the order of reaction is one.
Examples:
-
Acid hydrolysis of ester: CH3COOEt + H3O+ →CH3COOH + EtOH
-
Inversion of cane sugar:

-
Decomposition of benzenediazonium halides C6H5N=NCl +H2O → C6H5OH +N2 +HCl
These are the reactions in which more than one species is involved in the rate determining step but still the order of reaction is one.
Examples:
Acid hydrolysis of ester: CH3COOEt + H3O+ →CH3COOH + EtOH
Inversion of cane sugar:

Decomposition of benzenediazonium halides C6H5N=NCl +H2O → C6H5OH +N2 +HCl
Half – Life of a nth Order Reaction:
kt1/2 = (2n-1-1)/(n-1)[A0]n-1
Where, n = order of reaction ≠1
kt1/2 = (2n-1-1)/(n-1)[A0]n-1
Where, n = order of reaction ≠1
Parallel Reactions:
The reactions in which a substance reacts or decomposes in more than one way are called parallel or side reactions.
 If we assume that both of them are first order, we get.
If we assume that both of them are first order, we get.
![-\frac{d[A]}{dt} = (k_1 +k_2) [A] =k_{av}[A]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex-_fracdadtk_1k_2ak_ava.jpg) k1 = fractional yield of B × kav
k2 = fractional yield of C × kav
If k1 > k2 then
A → B main and
A → C is side reaction
Let after a definite interval x mol/litre of B and y mol/litre of C are formed.
k1 = fractional yield of B × kav
k2 = fractional yield of C × kav
If k1 > k2 then
A → B main and
A → C is side reaction
Let after a definite interval x mol/litre of B and y mol/litre of C are formed.
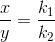 i.e
i.e
![\frac{\frac{d[B]}{dt}}{\frac{d[C]}{dt}} =\frac{k_1}{k_2}](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_frac_fracdbdt_fracdcdt_frack_1k_2.jpg) This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning ) is a constant equal to k1/k2.
This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning ) is a constant equal to k1/k2.

The reactions in which a substance reacts or decomposes in more than one way are called parallel or side reactions.

If we assume that both of them are first order, we get.
![-\frac{d[A]}{dt} = (k_1 +k_2) [A] =k_{av}[A]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex-_fracdadtk_1k_2ak_ava.jpg)
k1 = fractional yield of B × kav
k2 = fractional yield of C × kav
If k1 > k2 then
A → B main and
A → C is side reaction
Let after a definite interval x mol/litre of B and y mol/litre of C are formed.
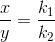
i.e
![\frac{\frac{d[B]}{dt}}{\frac{d[C]}{dt}} =\frac{k_1}{k_2}](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_frac_fracdbdt_fracdcdt_frack_1k_2.jpg)
This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning ) is a constant equal to k1/k2.


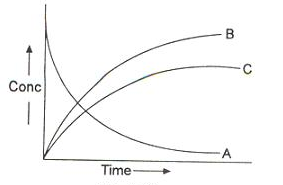
Sequential Reactions:
This reaction is defined as that reaction which proceeds from reactants to final products through one or more intermediate stages. The overall reaction is a result of several successive or consecutive steps.
A → B → C and so on

![-\frac{d[A]}{dt} = k_1[A]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex-_fracdadtk_1a.jpg) …....(i)
…....(i)
![\frac{d[B]}{dt} = k_1[A]-K_2[B]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_fracdbdtk_1a-k_2b.jpg) …......(ii)
…......(ii)
![\frac{d[C]}{dt} = k_2[B]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_fracdcdtk_2b.jpg) ….......(iii)
Integrating equation (i), we get
….......(iii)
Integrating equation (i), we get
![[A]-[A]_oe^{-k_1t}](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latexa-a_oe-k_1t.jpg)
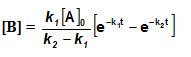
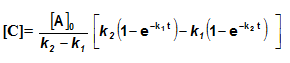
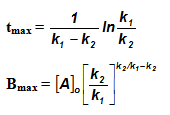
This reaction is defined as that reaction which proceeds from reactants to final products through one or more intermediate stages. The overall reaction is a result of several successive or consecutive steps.
A → B → C and so on

![-\frac{d[A]}{dt} = k_1[A]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex-_fracdadtk_1a.jpg) …....(i)
…....(i)![\frac{d[B]}{dt} = k_1[A]-K_2[B]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_fracdbdtk_1a-k_2b.jpg) …......(ii)
…......(ii)![\frac{d[C]}{dt} = k_2[B]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_fracdcdtk_2b.jpg) ….......(iii)
….......(iii)
Integrating equation (i), we get
![[A]-[A]_oe^{-k_1t}](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latexa-a_oe-k_1t.jpg)
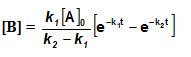
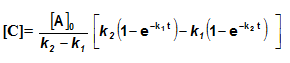
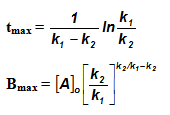

Arrhenius Equation:
k = A exp(-Ea/RT)
Where, k = Rate constant
A = pre-exponential factor
Ea = Activation energy
k = A exp(-Ea/RT)
Where, k = Rate constant
A = pre-exponential factor
Ea = Activation energy
Temperature Coefficient:
The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperature differing by 10oC.
μ = Temperature coefficient= k(r+10)/kt
Let temperature coefficient of a reaction be ' μ ' when temperature is raised from T1to T2; then the ratio of rate constants or rate may be calculated as
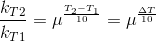
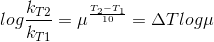
![\frac{k_T_2}{k_T_1}= antilog[\frac{\Delta T}{10 }] log\mu](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_frack_t_2k_t_1antilog_frac_deltat10log_mu.jpg) Its value lies generally between 2 and 3.
Its value lies generally between 2 and 3.
The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperature differing by 10oC.
μ = Temperature coefficient= k(r+10)/kt
Let temperature coefficient of a reaction be ' μ ' when temperature is raised from T1to T2; then the ratio of rate constants or rate may be calculated as
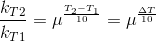
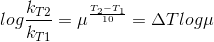
![\frac{k_T_2}{k_T_1}= antilog[\frac{\Delta T}{10 }] log\mu](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_frack_t_2k_t_1antilog_frac_deltat10log_mu.jpg)
Its value lies generally between 2 and 3.
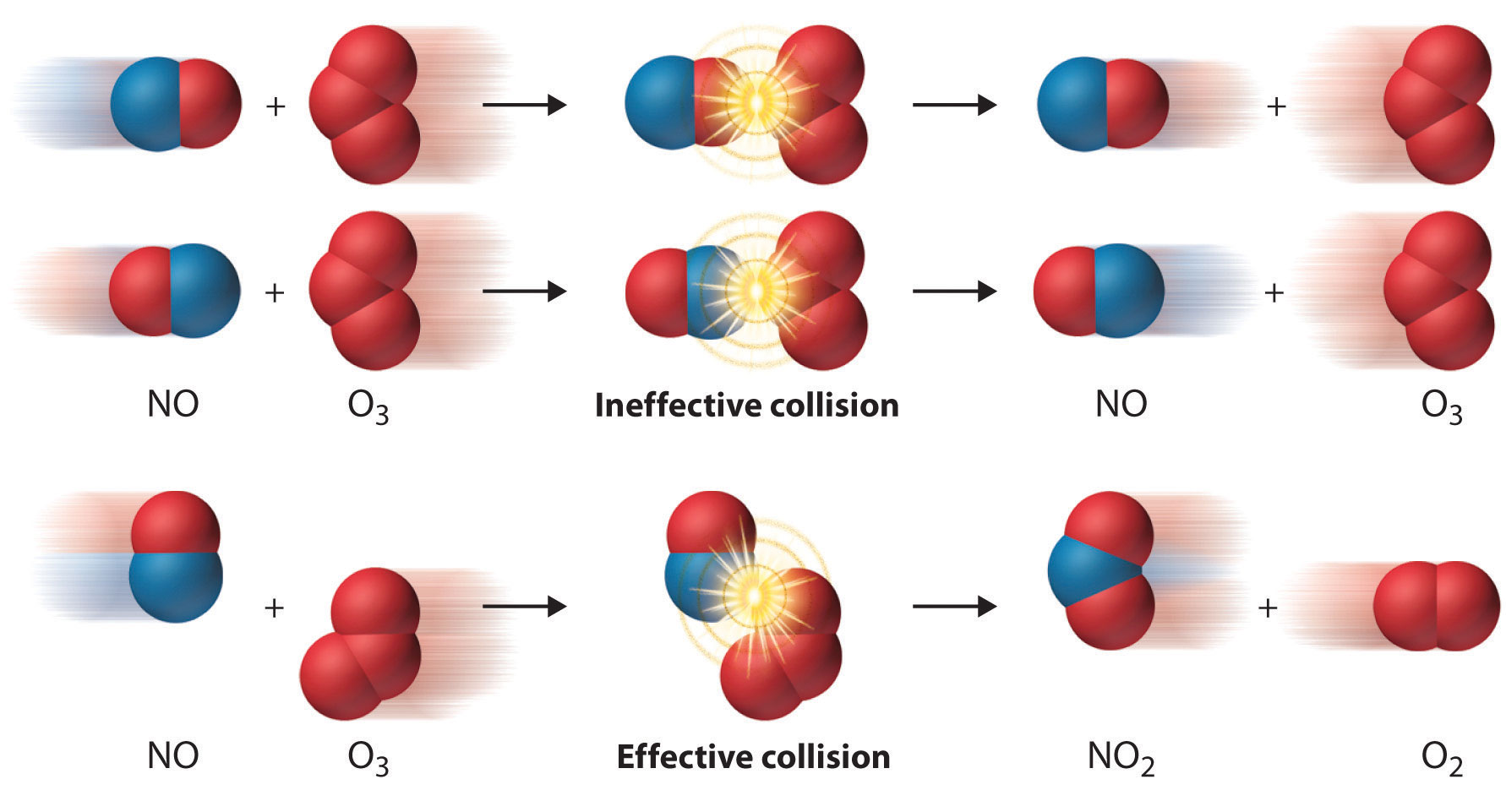
Collision Theory of Reaction Rate
- A chemical reaction takes place due to collision among reactant molecules.
- The number of collisions taking place per second per unit volume of the reaction mixture is known as collision frequency (Z).
- The value of collision frequency is very high, of the order of 1025 to 1028 in case of binary collisions.
- Every collision does not bring a chemical change.
- The collisions that actually produce the products are effective collisions.
- The effective collisions which bring chemical change are few in comparison to the form a product are ineffective elastic collisions, i.e., molecules just collide and
- disperse in different directions with different velocities.
- For a collision to be effective, the following two barriers are to be cleared.
- Energy Barrier
- Orientation Barrier
Radioactivity:
All radioactive decay follow 1st order kinetics
For radioactive decay A ->B
-(dNA/dt) =l NA
Where, l = decay constant of reaction
NA = number of nuclei of the radioactive substance at the time when rate is calculated.
Arrhenius equation is not valid for radioactive decay.
Integrated Rate Law: Nt = Noe-lt
Half Life: t1/2= 0.693/λ
Average life time: Life time of a single isolated nucleus, tav= 1/λ
Activity: Rate of decay
A = dNA/dt, Also, At = Aoe-lt
Specific Activity: activity per unit mass of the sample.
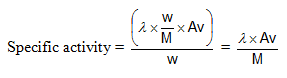
Units: dps or Becquerre



No comments:
Post a Comment